Trajectory Error |
|||
 Previous |
 Next |
|
|
Total Trajectory Error
A common question arises when running trajectories...."What is the error associated with a given trajectory calculation." Overall, from the literature, one can estimate the total error to be anywhere from 15 to 30% of the travel distance. The total error is composed of four error components:
- physical error due to the inadequacy of the dataís representation of the atmosphere in space and time,
- computational error due to numerical inaccuracies,
- measurement errors in creating the modelís meteorological data fields,
- forecast error if using forecast meteorology.
The physical component of the error is related to how well the numerical fields estimate the true flow field. There is no way of knowing this error without independent verification data.
The computational component of the error is composed of the integration error (part of which is due to truncation) and a data resolution error, i.e., trying to represent a continuous function, the atmospheric flow field, with gridded data points of limited resolution in space and time. The integration error can be estimated by computing a backward trajectory from the forward trajectory endpoint. The error is then 1/2 the distance of the final endpoint and the starting point. The resolution error can be estimated by starting several trajectories about the initial point (offset in the horizontal and vertical). The divergence of these trajectories will give an estimate of the uncertainty due to divergence in the flow field. An initial offset should be used that is comparable to the estimated integration error. One component of the resolution error that is difficult to estimate relates to the size and speed of movement of various flow features through the grid. There should be sufficient number of sampling points (in space and time) to avoid aliasing errors. Typically a grid resolution of "x" can only represent wavelengths of "4x". This error will be a function of the meteorological conditions.
Integration Error Example
The integration error component of the numerical error can be estimated by running a forward and backward trajectory to the origin point.† See Example 3 Powerpoint (Ex3_hysplit.ppt)or,
| view the previous 700 hPA isobaric example trajectory endpoints file, and use the final position (69.866N, 16.833W, 2797.8 m AGL) as the starting point (on the 23th 0000 UTC) for a backward trajectory calculation.† If performing this calculation using PC HYSPLIT, insure that the trajectory endpoints file names are different for both the forward and backward calculations so that both trajectories can be plotted on the same map. Unfortunately, multiple independent trajectories cannot be plotted on the same map using HYSPLIT-WEB. |
|
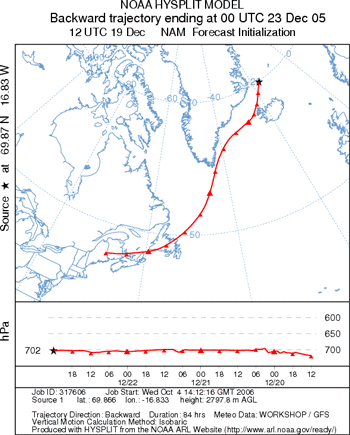
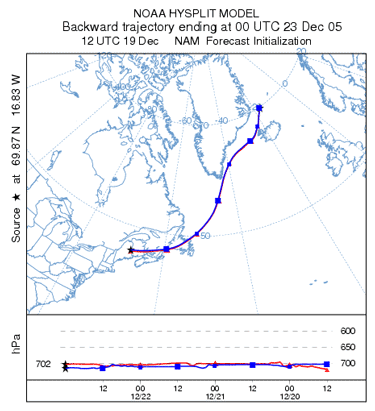
| The plot on the left below is the backward trajectory. Note how the
return trajectory endpoint is very close to the initial origin point indicating very little
integration error. The plot to the right was generated by downloading both trajectory endpoints
files and plotting them on the same map using PC HYSPLIT. You can see that the model
automatically switched from the GFS back to the NAM 40 km grid at 0600 UTC on December 20
by viewing the
backward endpoints file. |
|
|
 |
Resolution Error Example
| As mentioned before, a greater source of error, resolution error, is due to the difficulty in representing atmospheric variables, which are continuous in space and time, by discrete data points on a grid.† This error is difficult to quantify, but a sense of the error can be determined by running trajectories using several different sources of meteorological data.† In the adjacent calculation, trajectories have been computed using meteorological data from NAM(12 km)/GFS (red), RUC/GFS (blue), and MM545/GFS (green). After the first 36 hours, differences between trajectories are much greater than the numerical error.† Note that the green trajectory went up near the end because it hit Greenland (HYSPLIT is terrain following). These calculations are more consistent than most simulations due to the isobaric assumption. | 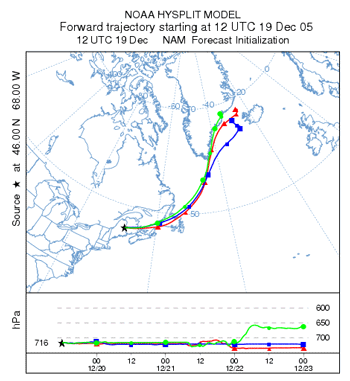 |
 Previous |
 Next |