Modeling Particle Motion or |
|||
 Previous |
 Next |
|
|
| To compute air concentrations it is necessary to
follow all the particles needed to represent the pollutant distribution
in space and time. This can be done explicitly by following the
trajectory of each particle, where a random component is added
to the mean velocity (from the meteorological model), to define
the dispersion of the pollutant cloud. In the horizontal, the
computations can be represented by the following equations: X(t + Δt) = Xmean(t + Δt) + U'(t + Δt)Δt, U'(t + Δt) = R(Δt) U'(t) + U''(1 - R(Δt)2)0.5, R(Δt) = exp(-Δt/TLx), U'' = σuλ where λ is a random number with 0 mean and σ of 1. |
The computations can be simplified, if instead of
modeling the motion of each particle, we compute the trajectory
of the mean particle position and the particle distribution. The
standard deviation of the particle distribution could be computed
from all the particles, _______ σ2 = (Xi-Xm)2 or it can be computed without following individual particles by assuming a distribution shape (puff) and relationship to the local turbulence. Many different formulations can be found in the literature. dσh/dt = √2 σu σu = (Kx / TL)0.5 These computations are set in the Advanced / Configuration Setup / Concentration menu, which creates the SETUP.CFG file. |
Below, note the initial differences between the simulation using the 3D particle distribution (left) and the top-hat puff center postion method (right). Without the random motion component the top-hat puff positions follow a straight line during the initial few hours until vertical motions or horizontal divergence begins to act on the particles. In this particular case the main reason for the sudden expansion of the puff-particles is that they have mixed to higher levels and we are seeing the differential horizontal advection acting upon the particles.
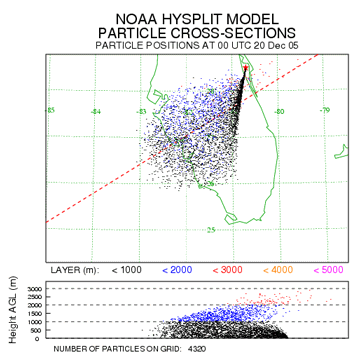 3-D Particle distribution |
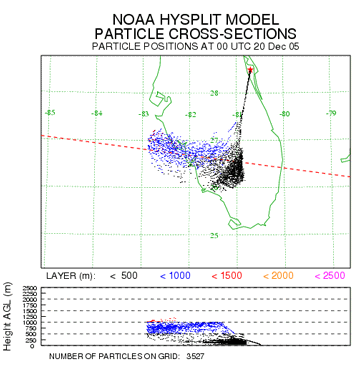 Top-Hat Puff center positions |
 Previous |
 Next |